| Вообще-то у фракталов долгая история. Началась она во времена Фибоначчи (Leonardo Pisano, Fibonacci, родился около 1170 — умер после 1228), который первым заинтересовался размножением кроликов. Некто поместил пару новорождённых кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Эта задача производит первый в истории ряд чисел с некоторыми фрактальными свойствами. Сейчас фракталами обычно считают бесконечно повторяющиеся самоподобные фигуры, например, очертания берега моря. Интересно, что впервые с этим фактом встретились в XIX веке. Адмиралтейству Великобритании захотелось написать на карте “общая длина береговой линии Британских островов равна стольким-то милям”. Они назначили кого-то для этой работы, снабдили его картами и курвиметром и — вперёд! И тогда выяснилось, что искомая длина сильно зависит от масштаба. Когда мы увеличиваем масштаб, на карте возникают всё новые и новые бухты, бухточки и бухтёшечки, и общая длина таким образом возрастает потенциально до бесконечности. |
Мои же взаимоотношений с ними восходят ко
времени учёбы в МАИ. Нам рассказывали много всего
интересного о математике. В частности, строили
примеры фигур, периметр которых бесконечен, а
площадь конечна или даже равна нулю. Тогда как
раз появились вычислительные машины, которые
позволили наглядно показывать картинки, на
ручное построение которых потребовалось бы
затратить сотни лет. В итоге получалась своего
рода компьютерная живопись. И кто бы мог
подумать, что к такому результату приведут
исследования задач вроде исчисления популяции
кроликов в зависимости от количества доступного
корма. К моему великому сожалению, в то время я не
оценил перспектив и занялся совсем другим. Это
одно из немногого, о чём я действительно жалею
сегодня. Тогда вся эта теория только начинала
активно развиваться, и там довольно легко было
получить какие-нибудь значимые результаты. Но
вместо меня их получил
Мандельброт
Потом через много лет я взял у приятеля Володи Филиппова книгу “Красота фракталов” и понял, какую ошибку совершил, но пить боржом было уже, как всегда, поздно. Поэтому я написал для собственного удовольствия программу, которая умеет рисовать вот такие картинки.
К сожалению, рисунки несколько пострадали при сжатии jpeg'ом. На самом деле они лучше. Некоторые из них можно использовать как обои рабочего стола. Когда-нибудь потом переделаю их в gif, как следующие два:

Вообще в природе множество процессов управляются фрактальными законами. Кроме уже упомянутой пары кроликов и длины береговой линии Британии, фрактальной природой обладают растения, облака, кристаллы и многое другое, я бы даже сказал, почти всё на свете. Одна из современных космогонических теорий представляет Вселенную в виде бесконечной последовательности шаров, растущих на границах вселенных большего размера. Получается типично фрактальная конструкция.
В доказательство этого привожу несколько картинок.
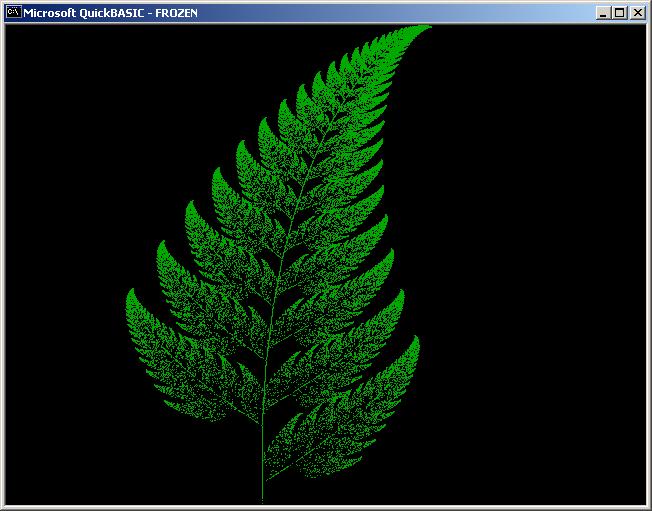
Как вам это нравится? Программа на Бейсике, которая рисует эту картинку состоит всего из нескольких строк. Она здесь. А такие математические деревья рисует мой screen saver:



А вот крепость Bourtange в Нидерландах. Ну, кто
скажет, что это не фрактал?

И крепость, и цветок кактуса

построены по плану вот этого фрактала:
А уж вулкан Taranaki в Новой Зеландии вообще явный родственник множеству Мандельброта.
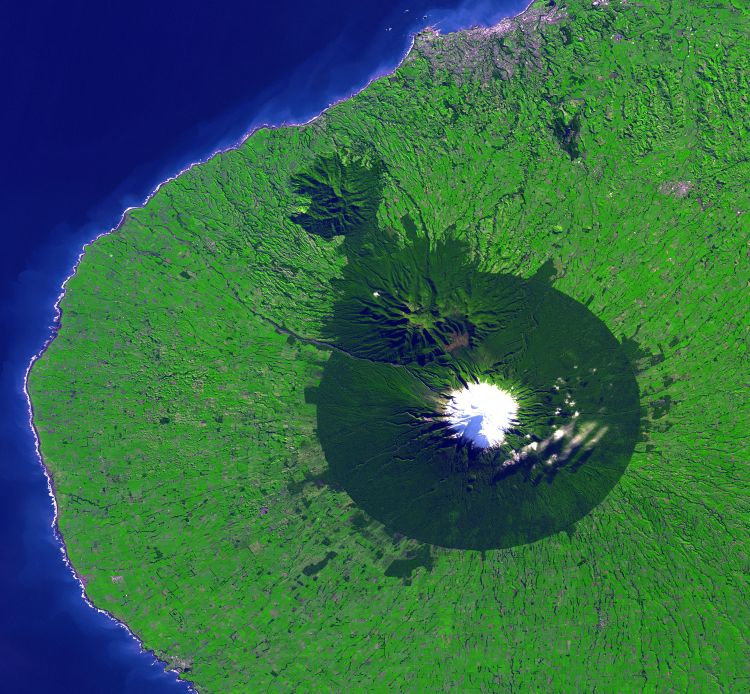

Люблю фракталы. Кстати, и причёска Мандельброта на портрете в начале этой страницы тоже имеет явно фрактальную природу. Мне так кажется, по крайней мере.
Упомянутую выше книгу я нигде не нашёл, поэтому интересующимся рекомендую эту.
И вот красивый фильм от телеканала Культура:
Фильм сделали в память о Бенуа Мандельброте в 2010 году. Не обращайте внимания
на то, что диктор коверкает некоторые новые для себя слова.
Фильм всё равно хорош.
| Last modified 2021-09-01 |